Adding new models

IMPORTANT NOTE

The shift to CmdStanR (using the instantiate package; as opposed to RStan) resulted in some changes to the model implementation. Recent version of CmdStanR seem not to handle include statements properly when models are compiled, and so the the utility, updating, and temperature function modules are now included directly within the fit_igt.stan, likelihood_igt.stan, and simulate_igt.stan model files.

The explanations below remain essentially correct, but the modifications need to be made directly in the function() blocks of the three model files, rather than in e.g. utilityWrapper.stan and utilityFunctions.stan. The wrapper and function files remain included in the package in src/stan/include pending the resolution of the issues with CmdStanR.

Package structure

Adding new model components (e.g. new utility functions) involves two broad steps:

Making the component available to stan, which is responsible for all model simulation and fitting.
Updating iowa’s internal information about the model component, including parameter names, bounds, etc.

Although the actual process of adding a new component is slightly tedious, the ultimate goal is that, once added, the new component can be used with all package functions (and combined with all other components) with a minimum of thought or fuss.

Internal package structure

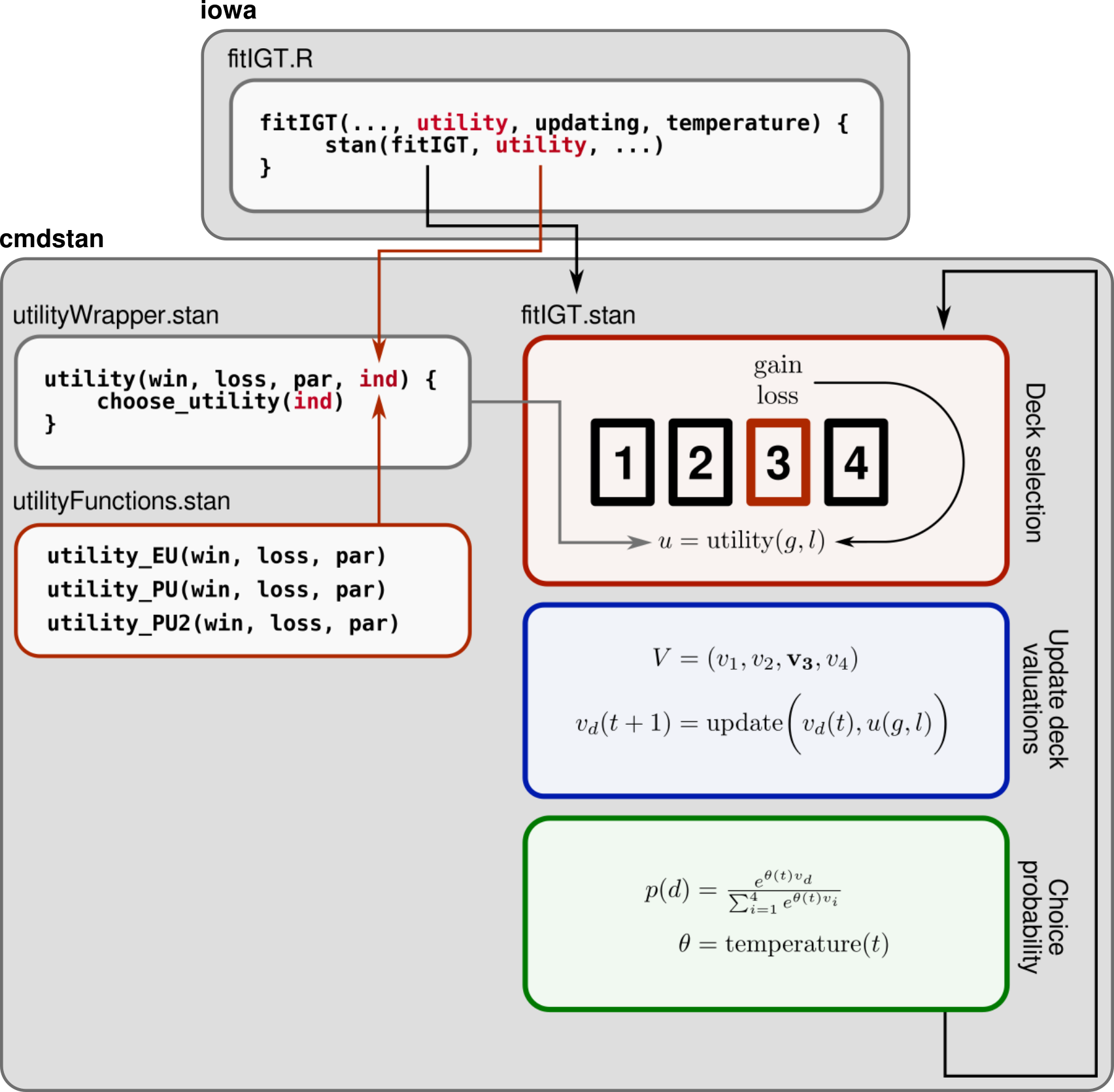
The general structure of the package is as follows:

The package interfaces with CmdStanR models through wrapper functions such as simulateIGT() and fitIGT().
Models are implemented in src/stan/<modelfile>>.stan.
The actual component functions (e.g. the specific utility function) are passed internally as data to the stan model, which are then imported from a separate .stan file. These separate files are stored in src/stan/include, with the names e.g. utilityFunctions.stanfunctions.

For example, src/stan/fitIGT.stan – which is responsible for model fitting – specifies a general model as follows:

// Likelihood
for (t in 1:NUM_TRIALS){

    // Compute temperature
    theta = temperature(t, temperature_params, TEMPERATURE_FUNCTION);

    // Draw card
    choice[t] ~ categorical_logit(theta * V);

    // Compute utility
    U = utility(win[t], loss[t], utility_params, UTILITY_FUNCTION);

    // Update deck values
    V = updating(V, U, choice[t], updating_params, UPDATING_FUNCTION);
}

On trial t, the utility of the outcome is evaluated through the function

utility(win[t], loss[t], utility_params, UTILITY_FUNCTION);

where utility is imported from src/stan/include/utilityWrapper.stanfunctions, and is defined by

real utility(real win, real loss, array[] real par, int ind){

    if (ind == 1){
        return utility_EU(win, loss, par);
    } else if (ind == 2){
        return utility_PU(win, loss, par);
    } else if (ind == 3){
        return utility_PU2(win, loss, par);
    } else {
        return 0;
    }
}

Note that this function is just a general wrapper that calls one of several utility functions depending on the integer argument ind. In turn, all utility functions are defined in inst/stan/include/utilityFunctions.stan.

As an example, the EU and PU utility are defined by:

// EU utility function (used in EV model)
real utility_EU(real win, real loss, array[] real par) {
    return (1-par[1]) * win - par[1] * loss;
}

// Prospect utility function
real utility_PU(real win, real loss, array[] real par) {
    real net = win - loss;
    if (net >= 0){
        return pow(net, par[1]);
    } else {
        return -par[2] * pow(abs(net), par[1]);
    }
}

Note an important point: All utility functions have exactly the same signature; that is real win, real loss, array[] real par.

The package in turn contains a modelDetails object contained in R/sysdata.rda. This structure is a nested list containing information about each model component; such as its required parameters, and any necessary (or default) bounds.

The structure of this list is as follows:

modelDetails
.  utility
. .  EU
. . .  index = 1
. . .  pars
. . . .  w
. . . . .  bounds = c(0,1)
. . . . .  default_bounds = c(0, 1)
. . . . .  description = "Win/loss weighting"
. . . . .  index = 1
. .  PU
. . .  index = 2
. . .  pars
. . . .  A
. . . . .  bounds = c(0, Inf)
. . . . .  default_bounds = c(0, 1)
. . . . .  description = "Concavity of utility function"
. . . . .  index = 1
. . . .  L
. . . . .  bounds = c(0, Inf)
. . . . .  default_bounds = c(0, 5)
. . . . .  description = "Loss aversion"
. . . . .  index = 2

That is, it has fields utility, updating, and temperature; each of which is a named list with fields corresponding to each included function. The field index indicates the corresponding value of ind in the stan wrapper function (e.g. utility(..., ind = 1) chooses the EV utility), while the index within each parameter field specifies the position of each parameter in the par argument. The parameter fields also contain entries giving parameter bounds (outside of which the package will throw an error), as well as default bounds used for model fitting if the user does not specify their own.

The general structure of the package program is illustrated below, using the utility function as an example:

Implementing a new model component

Adding a new utility function to iowa now involves the following steps:

Add the function to src/stan/include/utilityFunctions.stanfunctions, making sure that it matches the required signature.
Add a new if statement to src/stan/include/utilityWrapper.stanfunctions, corresponding to the next highest value of ind.
Add a new field to modelDetails in the utility field – named with the unique keyword of the new utility function – and populate it with the necessary fields (i.e. one subfield for each parameter, each with the required fields bounds and default_bounds). The index field must correspond to the value of ind which calls the new utility function in step (2).
Resave modelDetails to R/sysdata.rda using save(modelDetails, file = 'R/sysdata.rda').

After the package is recompiled, the new utility function should be ready for use.

The steps for adding new updating or temperature functions are essentially identical, mutatis mutandis.

Corson N. Areshenkoff

2024-08-13

IMPORTANT NOTE

Package structure

Internal package structure

Implementing a new model component